细粉加工设备(20-400目)

我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。

MTW系列欧版磨粉机

稀油润滑系统，新型吊挂式笼式选粉机结构设计

LM立式辊磨机

采用新型碾磨装置自动化电控系统

5X系列欧版智能磨粉机

大型规模化环保智能磨粉机优选设备

LM矿渣立式磨

LM矿渣立式磨集破碎、干燥、粉磨、分级输送于一体

立式磨煤机

烘干与制粉二合一可边磨边烘干

雷蒙磨粉机

工业磨粉设备先驱，经济实用

更多了解

超细粉加工设备(400-3250目)

LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。

LUM超细立磨

LUM超细立磨结合现代磨粉理念

MW环辊微粉磨

采用新型碾磨装置自动化电控系统

粗粉加工设备(0-3MM)

兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。

LM砂粉立磨

大型效率与节能双高型砂粉制备产品

在三角形abc中ab=ac 角bac=120° p为bc的中点

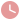
如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB

2016年11月13日 — 如图，在 ABC中，∠BAC＝120°，P为 ABC内一点，求证：PA＋PB＋PC＞AB＋AC证明：以AC为边向外作正 ACE，则E在BA延长线上，如图，作$AF\bot BC$于$F$，作$EG\bot AC$于$G$$\because \triangle ABC$中，$\angle BAC=120^{\circ}$，$AB=AC$$\angle B=\angle C=30^{\circ}$在$R{t}\triangle CEG$ 如图， ABC中，∠ BAC=120°，AB=AC，点D为BC边上的点解：（1）∵AB＝AC，∠BAC＝120°， ∴∠ABC＝∠ACB＝30°， ∵∠ACM＝∠ACB， ∴∠ACM＝∠ABC，在 ABD和 ACE中， ∴ ABD≌ ACE （2）由（1）可知， ABD≌ ACE， [题目]在 ABC中AB＝AC∠BAC＝120°以CA为边在∠ACB的 (本题满分8分)如图,在 ABC中,∠BAC=120°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA(1)试求∠DAE的度数(2)如果把题中“AB=AC”的条件去掉,其余条件不变,那如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上

在三角形ABC中AB等于AC,角BAC等于120度,AB的垂直平分线交BC

2010年10月17日 — 在三角形ABC中AB等于AC,角BAC等于120度,AB的垂直平分线交BC于D,且BD等于6厘米求DC的长解题思路：利用特殊角，运用余弦定理，先求出AB长度，然 2023年5月28日 — 30度角形成正三角形有两种方式，一是沿其某条夹角边翻折，或是作其对边与本30度角顶点所成三角形的外心，这都能形成正三角形，好不好用取决于其对称轴是否与图形的重要轴线重合。已知：在三角形ABC中，AB=AC,角BAC=20度，D点第1章解三角形 1 (2023• 乙卷) 在 ABC 中，已知 ∠BAC = 120°，AB = 2，AC = 1． (1) 求 sin∠ABC； (2) 若 D 为 BC 上一点．且 ∠BAD = 90°，求 ADC 的面积．解：(1) 在 ABC 2023年全国高考数学真题分类汇编大题解析版【第1章解三角解答一举报证明：连接AF， ∵AB=AC，∠BAC=120°， ∴∠B=∠C=30°， ∵EF为AB的垂直平分线， ∴BF=AF， ∴∠BAF=∠B=30°， ∴∠FAC=120°30°=90°， ∵∠C=30°， ∴AF= 1 2 如图在 ABC中，AB=AC，∠BAC=120°，EF为AB的垂直

如图，在等腰三角形ABC中，AB=AC，∠BAC=120°，AD⊥BC

如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;② OPC是等边三角如图，在 ABC中，AB=AC，∠BAC=80°，O为 ABC内一点，且∠OBC=10°，∠OCA=20°，求∠BAO的度数．解：作∠BAC的角平分线与CO的延长线交于点D，连接BD，则∠BAD=∠DAC ∵AB=AC，∠BAD=∠DAC，AD=AD， ∴ ABD≌ ACD， ∴BD=CD，∠ 如图，在 ABC中，AB=AC，∠BAC=80°，O为 ABC内一点 [分析](1)求出∠ABC的度数,即可求出答案;(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°﹣α,且 BCD为等边三角形,证 ABD≌ ACD,推出∠BAD=∠CAD=∠BAC=α,求出∠BEC=α=∠BAD,证 ABD≌ EBC,推出AB=BE即可;(3)求出∠ 在 ABC中,AB=AC,∠BAC=α(0°百度教育 Baidu Education如图,三角形ABC中,AB=AC,角BAC等于120度,EF是AB的垂直平分线,EF交BC于F,交AB于E求证BF=二分之一FC 如图所示， ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．如图在 ABC中，AB=AC，∠BAC=120°，EF为AB的垂直

已知如图三角形ABC中,AB=AC,角BAC=120度,DE垂直平分

2012年10月11日 — ab=ac 角bac=120度所以角abc=角acb等于60度所以角edca等于30度由30度所对的边等于斜边的一半加上勾股定理即可算出ce 也可以得出ac 做垂线垂直于bc再次利用由30度所对的边等于斜边的一半加上勾股定理（或者正余弦函数）即可算出bc也就（1）证明：如图，连接CD，交AB于点F，AD=BD点C和点D均在线段AB的垂直平分线上直线CD为线段AB的垂直平分线为等腰直角三角形(2)如（1）中图所示若，则线段AE的长为1(1)连接CD，交AB于点F，则由线段垂直平分线的判定定理可得，直线CD是线段AB的如图所示，在三角形ABC中，角ABC＝90度，AC=BC,D为 2007年3月17日 — 已知三角形ABC中,AB=9,AC=15,角BAC=120度,三角形ABC所在平面外一点P到把P点做为球心,那么（距离）半径是14，A,B,C就在球面上 BC^2=AB^2+AC^22AC*AB*COS120 所以BC=21 那 ABC 已知三角形ABC中,AB=9,AC=15,角BAC=120度,三角形ABC 【解析】【分析】 (1)根据线段垂直平分线的性质可得EA=EB，进一步即可求得结果； (2)先根据等腰三角形的性质和三角形的内角和定理求出∠ABC的度数，再利用等边对等角求出∠EBA的度数，即可求出结果【详解】解：(1)∵DE是AB的垂直平分线，∴EA=EB，【题文】已知：如图，在 ABC 中， AB = AC， AB 的垂直

如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D

2017年9月2日 — 如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，OP与AC相交与点M，则下列结论：①点O是 PBC的外心；② MAO∽ MPC；③AC=AO+AP；④S ABC=45S四边形AOCP．其中正确的2014年3月19日 — 如图，在 ABC中，AB=7，AC=11，点M是BC的中点，AD是角BAC的平分线，MF平行于AD延长CA到E，使得CF=FE。连BE，由M是BC的中点，F是CE的中点，∴CF=1#47;2CE，FM‖AD‖BE，只要知道CE，CF就知道了。如图，在 ABC中，AB=7，AC=11，点M是BC的中点，AD是 2012年5月1日 — 在 ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作 ADE，解:∵BD⊥AD,BE⊥AC 已知角有关的联系，根据已知条件和全等三角形的判定定理，得出 ABD≌ ACE，再根据全等三角形中对应角在 ABC中，AB=AC，点D是直线BC上一点（不与B、C重合如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA 1试求角DAE的度数 2如果把试题中AB=AC的条件去掉,其余条件不变,那么角DAE的度数会改变吗?为什么?如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上

在三角形ABC中，AB=AC，角BAC=120度，D是BC中点

2010年11月11日 — 因为AB=AC，角BAC=120度，D是BC的中点，所以BD平分角A，角BAD=60度过D作DF平行AC交AB于F点，因为D是BC的中点，所以F为AB的中点，AF＝BF，DF是直角三角形ADB的斜边上的中线，DF=AF 所以三角形ADF是等边三角形，因为DE垂直BF，所以DE平分AF，即AE＝EF 2019年12月16日 — 如图，在三角形ABC中，AB=AC，角BAC=120度。 D,F分别为AB、AC的中点从AB=AC角BAC=120度可以得到角B=角C=30度DE垂直于AB，GF垂直于AC后D、F点分别为AB、AC中点最后得到角C=角B角BDE=角CFG=90度也可得角DEB=角CFG线BD=C如图，在三角形ABC中，AB=AC，角BAC=120度。D,F分别 2013年10月20日 — 如图，在三角形ABC中，AB=AC，角BAC=120度，EF是AB的垂直平分线，EF交BC于点F，连接AF已知 ABC中，AB=AC，∠BAC=120°所以，∠B=∠C=30°已知EF是AB的垂直平分线所以，FB=FA则，∠BAF=∠B=30°那么，∠CAF 如图，在三角形ABC中，AB=AC，角BAC=120度，EF是AB 在 ABC中,已知AB=AC=6,∠BAC=120°,BC=6,点D是BC边上的任意一动点,点B与点B′关于直线（1）作高线AP，根据直角三角形30度角的性质可得AP的长；（2）根据S AB'D=S ADB，可知S AB'D与S ADC至少有一个不会超过S ABC的一半完全 (14分)如图,在 ABC中,已知AB=AC=6,∠BAC=120°,BC=6,点D

如图,在三角形ABC中,AB=AC,作业帮

因为 AB=AC,角A=36度所以角ABC=角ACB=72度因为 CD平分角ACB 所以角BCD=角DCA=36度因为角A=36度所以角BCD=角A 因为角DBC=角ABC 所以三角形CDB相似于三角形ABC 所以 AB/BC=BC/BD 因为角DCA=36度,角A=36度所以角DCA=角A如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;② OPC是等边三角形;③AC=AO+AP;④ABC OCP S =S四边形其中所有正确结论的序号为( )P AB D A ①②③【题文】如图，在等腰三角形ABC中，AB=AC，∠BAC=120 连接,证明,利用等腰三角形的性质可判断结论①;由线段垂直平分线的性质定理,等腰三角形的判定与性质,三角形的内角和定理,角的和差求出∠APO与∠DCO的和等于30°,再证明是等边三角形,可判断结论②,③;, 在线段AC上截取AE=AP,连接PE,证明 APO≌ EPC可判断结论④如图,已知等腰 ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P 如图，在Rt ABC中，∠BAC=90°，AB=AC，点D是BC边上一动点，连接AD，把AD绕点A逆时针旋转90°，得到AE，连接CE，DE．点F是DE的中点，连接CF．（1）求证：CF= AD；（2）如图2所示，在点D运动的过程中，当BD=2CD时，分别延长CF，BA，相交于如图，在Rt ABC中，∠BAC=90°，AB=AC，点D是BC边上一

如图,在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D

如图,在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E,F,作PM∥AC, 百度试题结果12011年7月20日 — 如图所示,在三角形ABC中,AB等于AC,角BAC等于120度,D是BC的中点,DE垂直于AB于E,求证:EB等于3EA连接AD因D是BC中点，即BD=CD，AB=AC，AD=AD则三角形ADB全等ADC则角ADB=角ADC=180度/ 2=90度，角BAD=角CAD=120度/2 如图所示,在三角形ABC中,AB等于AC,角BAC等于120度,D是 2020年3月22日 — 如图，在 ABC中，∠BAC=120°，AB=AC，点M、N在边BC上，MN长为多少？其实这个题目也不是奥数，初二初三，期中期末考试经常可能遇到的题目，稍微有一点难度，另一位网友的解，计算错误，下面给出了一个不同的解法如图，在 ABC中，∠BAC=120°，AB=AC，点M、N在边BC 2021年12月15日 — 如图,在三角形ABC中,角BAC=60度,D是AB上一点,AC=BD,P是CD的中点求证:AP=2分之BC证明：延长AP，使PE=AP=1/ 2AE，连接BE ,CE因为P是CD的中点所以PC=PD因为角APC=角EPD (对顶角相等）所以AC=DE角PAC=角PED所以AC平百度首页商如图,在三角形ABC中,角BAC=60度,D是AB上一点,AC=BD,P

已知等腰三角形ABC,角BAC=120度,P为BC中点,拿着含30度

2014年3月6日 — 已知等腰三角形ABC,角BAC=120度,P为BC中点,拿着含30度的透明三角板，使30 度角的顶点我来答首页用户认证用户认证团队合伙人热推榜单企业媒体政府其他组织商城法律答题我的已知等腰三角形ABC,角BAC=120度,P为BC中点,拿着含30度如图，在 ABC和 ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°（1）当点D在AC上时，如图①，线段BD，CE有怎样的数量关系和位置关系？直接写出你猜想的结论；（2）将图①中的 ADE的位置改变一下，如图②，其他条件不变，则线段BD，CE有怎样的数量【题目】如图，在 ABC 和 ADE 中， AB=AC ， AD=AE 在 ABC中，AB＝AC，D是直线BC上一点，以AD为一边在AD的右侧作 ADE，使AE＝AD，∠DAE＝∠BAC，连接CE设∠BAC＝α，∠DCE＝β(1)如图①，点D在线段BC上移动时，角α与β之间的数量关系是，请说明理由；(2)如图②，点D在线段BC的在 ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD2012年10月2日 — 在 ABC中，BA=BC，∠BAC=α，M是AC的中点，P是线段BM上的动点，将线段PA绕点P顺时针旋转2α得到线段PQ．（1）若α=60°且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D，请补全在三角形ABC中,BA=BC,∠BAC=a,M是AC中点，P是线段BM

如图，在等腰三角形ABC中，AB=AC，AD⊥BC于点D，CG

A G B D C证明：连接CE，如右图所示，∵AB=AC，AD⊥BC，∴AD是∠BAC的角平分线，∴BE=CE，∴∠EBC=∠ECB，又∵∠ABC=∠ACB，∴∠ABC−∠EBC=∠ACB−∠ECB，即∠ABE=∠ACE，又∵CG∥AB，∴∠ABE=∠CGF，∴∠CGF=∠FCE，又∠FEC=∠CEG，∴ 2014年6月5日 — 如图，在三角形ABC中，AB=AC，角BAC=120°，D,E是边BC上的点，角DAE=60°答：1）见下图所示， AB'D'即 ACD'，点B'与点C重合2）因为： ABD≌ ACD' 所以：AD=AD'，BD=CD'，∠BAD=∠CAD 如图，在三角形ABC中，AB=AC，角BAC=120°，D,E是边如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点（不与 B、C重合），在AC上取一点E，使∠ADE=30°．（1）求证： ABD∽ DCE；（2）设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围；（3）当 ADE是等腰【题目】如图，在等腰三角形ABC中，∠BAC=120°，AB 2023年5月28日 — 如图所示，等腰三角形ABC的顶角C为20，D为BC上一点使得CD = AB, 求∠ADB 这道题尽管形式上不同于角格点问题，但利用全等三角形可轻松转为角格点问题。我们可以以CD为底边向A侧作ΔCDE ≌ 已知：在三角形ABC中，AB=AC,角BAC=20度，D点

在 ABC中，∠BAC=120°，AD为角平分线，AC=3，AB=6

2017年3月7日 — 在 ABC中，∠BAC=120°，AD为角平分线，AC=3，AB=6，则AD 的长是多少图百度首页商城注册登录资讯视频图片知道文库贴吧 2013年11月15日 — 如图，在 ABC中，AB=AC,∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F证明：BF=2CF如图，很显然角C=角B=30，又因为垂直平分线，所以三角形AEF全等于三角形CEF，AF=CF，所以角EAF=角C=30，角BAF=12030=90，角如图，在 ABC中，AB=AC,∠BAC=120°，AC的垂直平分线如图，已知 A B C 中，AB=AC=6cm，∠B=∠C，BC=4cm，点 D 为 AB的中点．（1）如果点 P 在线段 B C 上以 1cm/s 的速度由点 B 向点 C 运动，同时，点 Q 在线段 C A 上由点 C 向点 A 运动．①若点 Q 的运动速度与点 P 的运动速度相等，经过 1 秒如图，已知 ABC中，AB=AC=10cm，BC=8cm，点D为AB的已知：如图，在 ABC中，AB=AC，点D，E分别在边AC，AB上，且∠ ABD=∠ ACE，BD与CE相交于点O求证：（1）OB=OC；（2）BE=CD （1）证明：∵AB=AC， ∴∠ABC=∠ACB； ∵∠ABD=∠ACE， ∴∠OBC=∠OCB， ∴OB=OC （2）证明：如图， A E D 已知：如图，在 ABC中，AB=AC，点D，E分别在边AC

如图所示,在等腰 ABC中,AB=AC,∠B=50°,D为BC的中点,点E

如图所示,在等腰 ABC中,AB=AC,∠B=50°,D为BC的中点,点E在AB上,∠AED=73°,若点P是等腰 ABC的腰上的一点,则当 EDP为以DE为腰的等腰三角形时,∠EDP的度数是 34°或535°或100°或134° 2013年12月1日 — 在三角形abc中,ab等于ac,∠bac等于120°,ef为ab的垂直平分线,ef交bc于点f,交ab与点e,且,ef等于3∵角B=30度，三角形BEF是RT三角形∴BF=2EF=6，BE=3根号3∴AB=AC=6根号3根据余弦定理，cosA=（AB方+AC方BC方）/2AB 百度首页商城在三角形abc中,ab等于ac,∠bac等于120°,ef为ab的垂直平分（1）利用正弦定理将已知等式化简，再根据两角和的正弦函数公式及诱导公式变形，求出tanB的值，结合B为三角形的内角即可算出角B的大小；（2）利用余弦定理b 2 =a 2 +c 22accosB的式子，结合基本不等式加以计算可得ac≤4+2在三角形ABC中，内角A，B，C所对的边分别为a，b，c 2019年11月20日 — 例：如图在 ABC中，∠BAC=90，AB=AC，D为BC中点。 E，F分别是AB，CA延长线上的点，且BE=AF，求证 DEF为等腰直角三角形如图：在 ABC中，AB＝AC，∠BAC＝90，BF平分∠ABC，CD丄BF交BF的延长线于点D，求证：BF＝2CD 证老教师帮你总结，等腰三角形中作辅助线的六种常用方法

如图，在 ABC中，AB=AC，∠BAC=80°，O为 ABC内一点

如图，在 ABC中，AB=AC，∠BAC=80°，O为 ABC内一点，且∠OBC=10°，∠OCA=20°，求∠BAO的度数．解：作∠BAC的角平分线与CO的延长线交于点D，连接BD，则∠BAD=∠DAC ∵AB=AC，∠BAD=∠DAC，AD=AD， ∴ ABD≌ ACD， ∴BD=CD，∠ [分析](1)求出∠ABC的度数,即可求出答案;(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°﹣α,且 BCD为等边三角形,证 ABD≌ ACD,推出∠BAD=∠CAD=∠BAC=α,求出∠BEC=α=∠BAD,证 ABD≌ EBC,推出AB=BE即可;(3)求出∠ 在 ABC中,AB=AC,∠BAC=α(0°百度教育 Baidu Education如图,三角形ABC中,AB=AC,角BAC等于120度,EF是AB的垂直平分线,EF交BC于F,交AB于E求证BF=二分之一FC 如图所示， ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．如图在 ABC中，AB=AC，∠BAC=120°，EF为AB的垂直 2012年10月11日 — ab=ac 角bac=120度所以角abc=角acb等于60度所以角edca等于30度由30度所对的边等于斜边的一半加上勾股定理即可算出ce 也可以得出ac 做垂线垂直于bc再次利用由30度所对的边等于斜边的一半加上勾股定理（或者正余弦函数）即可算出bc也就已知如图三角形ABC中,AB=AC,角BAC=120度,DE垂直平分

如图所示，在三角形ABC中，角ABC＝90度，AC=BC,D为

（1）证明：如图，连接CD，交AB于点F，AD=BD点C和点D均在线段AB的垂直平分线上直线CD为线段AB的垂直平分线为等腰直角三角形(2)如（1）中图所示若，则线段AE的长为1(1)连接CD，交AB于点F，则由线段垂直平分线的判定定理可得，直线CD是线段AB的 2007年3月17日 — 已知三角形ABC中,AB=9,AC=15,角BAC=120度,三角形ABC所在平面外一点P到把P点做为球心,那么（距离）半径是14，A,B,C就在球面上 BC^2=AB^2+AC^22AC*AB*COS120 所以BC=21 那 ABC 已知三角形ABC中,AB=9,AC=15,角BAC=120度,三角形ABC 【解析】【分析】 (1)根据线段垂直平分线的性质可得EA=EB，进一步即可求得结果； (2)先根据等腰三角形的性质和三角形的内角和定理求出∠ABC的度数，再利用等边对等角求出∠EBA的度数，即可求出结果【详解】解：(1)∵DE是AB的垂直平分线，∴EA=EB，【题文】已知：如图，在 ABC 中， AB = AC， AB 的垂直 2017年9月2日 — 如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，OP与AC相交与点M，则下列结论：①点O是 PBC的外心；② MAO∽ MPC；③AC=AO+AP；④S ABC=45S四边形AOCP．其中正确的如图，在等腰 ABC中AB=AC，∠BAC=120°，AD⊥BC于点D

如图，在 ABC中，AB=7，AC=11，点M是BC的中点，AD是

2014年3月19日 — 如图，在 ABC中，AB=7，AC=11，点M是BC的中点，AD是角BAC的平分线，MF平行于AD延长CA到E，使得CF=FE。连BE，由M是BC的中点，F是CE的中点，∴CF=1#47;2CE，FM‖AD‖BE，只要知道CE，CF就知道了。2012年5月1日 — 在 ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作 ADE，解:∵BD⊥AD,BE⊥AC 已知角有关的联系，根据已知条件和全等三角形的判定定理，得出 ABD≌ ACE，再根据全等三角形中对应角在 ABC中，AB=AC，点D是直线BC上一点（不与B、C重合

定量给料机i滑石

河北张家口市白云石粉生产线全套设备

T型磨

山东滨州高钙粉价格

云南欧版磨粉机

XMW30立式离心研磨机

全新来自中国的矿石磨粉机那里有买的

模板矿石磨粉机山东产

石灰石粉碎机冶炼废渣回收用什么设备好

矿石磨粉机多少钱一台

水力切割破除钢筋混凝土

山东威海市白云石微粉磨生产设备

325目活性炭用什么雷蒙磨

zkr型碳酸钙高细立磨

时产30吨方解石粉碎设备

立式精矿磨矿机

用机矿石制粉可以种植天麻吗

广州日报曾向荣

95中速磨煤机高压油站常见故障95中速磨煤机高压油站常见故障95中速磨煤机高压油站常见故障

方解石矿开采需要什么设备

石灰石乐石粉碎场

微粉超细粉矿渣

山西临汾市白云石超细磨加工细度

办采矿权多久

整套立解石磨粉生产线机械

碳酸钙石灰石粉碎机冶炼废渣粉碎粉磨系统站

花岗闪长岩中速粉石灰石粉碎机

萤石开采前景

风电有市场吗

tsj1311