细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备,拥有多项国家专利,能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目,是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术,专注于400-3250目范围内超细粉磨加工,细度可调可控,突破超细粉加工产能瓶颈,是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势,产量高、破碎比大、成品率高,在粗粉加工方面成绩斐然。
AD平行BC
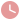
.jpg)
如图,在梯形ABCD中,AD平行BC,对角线AC与BD相较于
如图,在梯形ABCD中,AD平行BC,对角线AC与BD相较于点O,过点O作OE平行AD交AB于点E,若AD=3cm,BC=6cm,三角形AOD的面积为9cm 1,求三角形BOC和三角形DOC 解答一 举报 证明: 延长AE,交BC的延长线于点G ∵AD∥BC ∴∠D=∠GCE,∠DAE=∠G ∵EC=ED ∴ ADE≌ GCE ∴AE=GE ∵∠ABC=90° ∴AE=CE=BE(直角三角形斜边中线等于 已知,如图,梯形ABCD中,AD平行BC,∠ABC=90°,E为CD的中点 平行四边形是指有两组对边分别平行的四边形。 平行四边形的性质包括:1对边平行;2对角线互相平分;3相邻角互补;4对角线长度相等。 平行四边形的判定方法包括:1对边平 如图,在梯形ABCD中,AD∥BC,对角线AC⊥ BD,且AC=12 2012年5月16日 — 如图,已知AB=CD,AD=BC,那么AD与BC平行吗?请说明理由团队 俊狼猎英 为您解答~平行。 以下给出证明:因为AB=CD,AD=BC,所以四边形ABCD为平行四边形 如图,已知AB=CD,AD=BC,那么AD与BC平行吗?请说明理由

如图 已知AD平行BC百度知道
2014年8月7日 — 因为AD平行BC 所以角BCD+角ADC=180° 因为AB=DC 所以角ABD=角DCB 所以角ABC+角ADC=180° 又因为角ABC+角ABE=180° 所以角ABE=角ADC 在三 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=24 cm,BC=26 cm点P从A出发,以1 cm/s的速度向点D运动,点Q从点C同时出发,以3 cm/s的速度向点B运动,规定其中一个动点 【题文】如图,在四边形 ABCD 中,AD∥BC,∠B=90°,AB 2012年11月25日 — ∵在梯形ABCD中,AD平行BC,AE平分∠BAD,BE平分∠ABC,∴∠ABE+∠BAE=90°,∠AEB=90°,作AB中线EF,则EF=AF=BF 在梯形ABCD中,AD平行BC,AE平分∠BAD,BE平分∠ABC,求 2014年5月24日 — 已知,如图,AD平行BC,E是线段CD的中点,AE平分∠BA 356 更多类似问题 > 为你推荐: 特别推荐 “网络厕所”会造成什么影响? 新生报道需要注意什么? 华强北的二手是否靠谱? 癌症的治疗费用为何越来越高 已知 如图,AD平行BC,点E是DC的中点,AE平分角BAD

如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB
[答案](Ⅰ)见证明;(Ⅱ)(Ⅲ)[解析]分析]首先利用几何体的特征建立空间直角坐标系(Ⅰ)利用直线BF的方向向量和平面ADE的法向量的关系即可证明线面平行;(Ⅱ)分别求得直线CE的方向向量和平面BDE的法向量,然后求解线面角的正弦值即可;(Ⅲ)首先确定两个半平面的法向量,然后利用二面角的余弦值计算公式 [答案]6或7[解析]分析:当PD=CQ时可知四边形PQCD为平行四边形或四边形PQCD为等腰梯形,根据它们的性质可建立关于t的方程,解出即可详解:(1)当PD=CQ时,四边形PQCD是平行四边形;设运动时间为t秒,∴24t=3t解得t=6s,(2)当四边形PQCD是等腰梯形时,PQ=CD如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm 25解析:本题考查了切线的判定和性质、全等三角形的判定和 性质、等边三角形的判定和性质以及扇形面积的计算等 (1)观察图形,易得CD与⊙B相切要证明CD与⊙B相切, 因为CD与⊙B没有明确的公共点,所以可利用“ d=r^+ 的方 法证明点B到CD的距离等于⊙B的半径如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以 (12分)(2017•闵行区一模)如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且FG GD=AD CE(1)求证:AB∥CD;(2)如果AD2=DG•DE,求证:EG 2 CE 2=AG AC[解答]证明:(1)∵AD∥BC,∴ ADG∽ CEG,∴AD AG CE如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点

如图,已知:梯形ABCD中,AD‖BC,AB⊥BC,AD=CD=5,AB=4
2011年10月10日 — 1因为PE=CE,所以∠C=∠EPC,推出∠APB=∠C所以AP平行DC,那么ADCP是平行四边形 AP=DC=5,用勾股定理算出BP=3 2BP=3,PC=5所以BC固定BC=8 过点D,E分别做垂线垂直BC为F,H点则BF=5,CF=3 利用CE/CD=CH/CF 计算出CH=391.已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD 线上的一点向角的两边作垂线0PB两垂直A一对称2过角平分线上的一点作角平分线的垂线,一平行从而形成等腰三角形; 1.已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC (12分)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD,对角线AC与BD交于点E点F是线段EC上一点,且∠BDF=∠BAC(1)求证:EB2=E 百度试题 结果1 结果2 结果3 题目 (12分)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD,对角线AC与BD交于点E点F是线段 (12分)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD ∵AD∥BC ,∴∠ADE+∠C=180°,∵∠AFE+∠EFB=180°,∴∠EFB=∠C,∵BE平分∠ABC,∴∠EBF=∠EBC 考点点评: 此题考查了全等三角形的判定与性质以及平行 线的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用 如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于

如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=10cm,AD
分析:(1)用t表示出AP和BQ的长,然后根据梯形的面积公式进行解答, (2)过P作PN⊥BC于N,过D作DM⊥BC于M,根据题干条件求出MC的长,用t表示出QN的长,若梯形PQCD为等腰梯形,则QN=MC,列出等式解出t的值,(3)若 PQC的面积与 PCD的已知:如图在直角梯形ABCD中,AD平行于BC,角ABC等于90度,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M,点F在线段ME上 已知:如图在直角梯形ABCD中,AD平行于BC,角ABC等于90度 2012年2月21日 — 过D作BC的垂线交BC于F。因为AD平行于BC,角ABC=90度,DF垂直BC。所以四边形ABFD是平行四边形,所以AD=BF,又因为BC=2AD所以BF=FC,又因为DF垂直BC,所以DF是BC的垂直平分线,所以BD=DC,又因为OE平行于BC,所以BO=EC,所以四边形如图,在梯形ABCD中,AD平行BC,角ABC=90度,BC=2AD 试题分析:(1)作AH垂直于BC,垂足为H,如图1所示,由∠B=∠BCD=45°,得到三角形ABH为等腰直角三角形,由等腰梯形的两底之差的一半求出BH的长,即为AH的长,由BCBH求出HC的长,利用勾股定理求出AC的长,由AD与BC平行,得到一对内错角相等,再 已知,等腰梯形ABCD中,AD∥BC,∠B=∠BCD=45°,AD=3

在梯形abcd中,AD平行BC,对角线AC垂直BD,AC=8,BD=6,求
2016年5月22日 — 在梯形abcd中,AD平行BC,对角线AC垂直BD,AC=8,BD=6,求梯形的高过点D作DE‖AC,交ABC的延长线于点E 则四边形ACED是平行四边形 ∴DE=AC=8∵AC⊥BD ∴BD⊥DE ∵BD=6,根据勾股定理得BE=10设梯形的高为h在Rt ABC 中,利如图,在四棱锥PABCD中,AD//BC,∠ ADC=∠ PAB=90()° ,BC=CD=1/2AD,E、M分别为棱AD、PD的中点,PA⊥ CD.1证明:平面MCE如图,在四棱锥PABCD中,AD//BC,∠ ADC=∠ PAB=90 2017年9月12日 — 已知如图,AD平行BC,AB垂直BC,CD垂直ED,AD=2 如图,AD平行BC,AB垂直BC,CD垂直DE,CD等于ED 更多类似问题 > 为你推荐: 特别推荐 “网络厕所”会造成什么影响? 华强北的二手是否靠谱? 癌症的治疗费用为何越 已知如图,AD ∥ BC,AB⊥BC,CD⊥DE,CD=ED,AD=2 (1)法一、取PB中点G,连接AG,NG,由三角形的中位线定理可得NG∥BC,且NG=12BC,再由已知得AM∥BC,且AM=12BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;法二、证 如图,四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC

如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD
如图,已知AD∥BC,AB⊥AD,点E,F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E与点F关于BD对称,AC与BD相交于点G,则()A1+tan∠ADB 百度试题 结果1如图,在直角梯形ABCD中,AD∥BC(BC AD),∠ B=90°,AB=BC=12,E是AB上一点,且∠ DCE=45°,BE=4,求DE的长 过C作CG⊥AD,交AD延长线于GA D 如图,在直角梯形ABCD中,AD∥BC(BC AD),∠ B=90°,AB 根据AD∥BC,可求证∠ADB=∠DBC,利用BD平分∠ABC和等量代换可求证∠ABD=∠ADB,然后即可得出结论. 本题考点: 等腰三角形的判定与性质;平行线的性质.如图,AD∥BC,BD平分∠ABC.求证:AB=AD.作业帮(1)证明:∵E是AD的中点,∴AE=DE,∵AF∥BC,∴∠AFE=∠DBE,在 AEF和 DEB中⎧⎩⎨⎪⎪∠AFE=∠DBE∠DEB=∠AEFAE=DE,∴ AEF≌ DEB(AAS),∴AF=DB,∴四边形ADCF是平行四边形,∵∠BAC=90∘,D是BC的中点,∴AD=CD=12BC,∴四边形ADCF 如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE

已知:如图在梯形ABCD中,AD平行于BC,M,N分别是对角
2019年10月5日 — 证明:连接AM并延长交BC于E AD平行于BC,D为BD的中点 则:AM/ME=DM/MB=1,得AM=ME;同理可证:AD=BE 又点N是AC的中点,故MN是⊿AEC的 中位线 ∵AD//BC∴ AOD相似于 COB,根据面积的比等于相似比的 平方 ∴AD:BC=AO:CO=DO:BO=√9/16=3:4 又 AOB、 COB的底边AO、CO在同一直线上,高相等∴面积的比等于AO:CO=3:4 ,S 如图,已知梯形ABCD中,AD//BC,对角线AC与BD相交于点O 梯形的定义: 一组对边平行,另一组对边不平行的四边形叫做梯形.如图,在梯形ABCD中,AD ∥ BC,AB=CD,P为BC上任意 试题分析:(1)在梯形ABCD中,AD∥BC,要使四边形PQCD为平行四边形,即PD=QC 。因为: PD=ADAP=18t;QC=2t。则18t=2t,解得t=6s (2)四边形ABQP为矩形,则AP=BQ。所以AP=BCQC即t=212t。解得t=7s (3)梯形PQCD是等腰梯形,则如图 如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC
.png)
在梯形ABCD中,AD平行BC,AD等于1,BC等于4,角C等于70度
2012年5月19日 — 作辅助线:过A点作DC的平行线AE交BC于E。∵∠AEB=∠C=70° 且∠B=40° ∴∠BAE=180°-∠B-∠AEB=70° ∵∠AEB=∠BAE ∴AB=BE=BC-EC=BC-AD(AECD是平行四边形)2012年5月10日 — 在梯形abcd中 ad平行bc 角b等于90度 角c等于45 2 更多类似问题 > 为你推荐: 特别推荐 华强北的二手是否靠谱? 癌症的治疗费用为何越来越高? “网络厕所”会造成什么影响? 电动车多次降价,品质是否有保障 如图,在梯形ABCD中,AD平行BC,角B等于45度,角C等于120 2009年5月5日 — 连接AG并延长,交BC于M 易证 BGM与 AGD全等 所以AG=GM,AD=MB, FG是三角形AMB的中位线 FG=1/2BC=1/2(BCAD)已知:如图,在梯形ABCD中,AD平行于BC,E,F分别是AB,AC的中点,本题主要考查角平分线的性质,要求两平行线AD与BC间的距离,即就是求AD与BC 之间的垂线段的长度; 过点P作MN⊥AD,交AD于M点,交BC于N点,AD与BC之间的垂线长度即为线段MN的长度; 结果一 题目 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的 如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP

已知:如图,在梯形 ABCD 中, AD/\!/BC, AB⊥BC, AB=2
(1)首先过点D作DH⊥BC,垂足为点H,由,AB⊥BC,DH⊥BC,可求得DH的长,然后设CH=x,则 CD=2x,利用勾股定理即可求得方程:,解此方程即可求得答案; (2)首先取CD的中点F,连接EF,由梯形的中位线,可表示出EF的长,易得四边形ABHD是平行四边初中平行四边形的性质与判定是初中数学中的重要内容。平行四边形是指有两组对边分别平行的四边形。平行四边形的性质包括:1对边平行;2对角线互相平分;3相邻角互补;4对角线长度相等。(11分)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC 【答案】过点D做DE∥AC交BC的延长线于点E,得出平行四边形ADEC,根据等底等高的三角形面积相等得出 ABD和 DCE的面积相等 如图:在梯形ABCD中,AD∥BC,AD=2,AC=4,BC=6 【答案】过点N分别作NG∥AB,NH∥CD,得平行四边形ABGN和平行四边形DCHN,根据平行四边形的性质可得到 GNH为直角三角形,且MN为其斜边上的中线,由已知可求得AD的长,从而不难求中位线的长了.A D w w E F B C G M过点N分别作NG∥AB,NH∥如图,在梯形ABCD中,AD∥BC,∠B=30°,∠C=60°,E、F

如图,在梯形 ABCD 中, AD//BC, BC=3AD,点 E 是腰 AB
解:(1)延长BA、CD相交于点M.如图1:∵AD∥BC,∴ MAD∽ MBC,A D E B C 图1∴ADBC=MAMB=13.∴MB=3MA.设MA=2x,则MB=6x.∴AB=4x.∵BE=3AE,∴BE=3x,AE=x.∴BE=EM=3x,E为MB的中点.又∵CE⊥AB,∴CB=MC.又∵MB=MC 1 如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠A.A DB C 2 【题目】如图,已知AB=AC=AD,且ADBC,求证:∠C=2∠ DD B 3 【题目】如图,已知AB=AC=AD,且 AD∥BC ,求证:∠C=2∠ DBC 4 【题目】如图,已知AB=AC=A D且 AD∥BC ,求证:∠C如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D Baidu 梯形abCd中,AD平行BC对角线AC,BD相交于O,过点O做EF平行于AD交AB,CD于点EFOE与OF有什么关系为什么2求出OE比OD加上OF比BC的值梯形abCd中,AD平行BC对角线AC,BD相交于O,过点O做EF (1)过D作DH⊥BC,DH与EF、BC分别相交于点G、H,从而判定四边形ABHD是矩形,在RT DHC中求出CH的长,利用AD=BH=BCCH可得出AD的长. (2)首先确定PM=PN,过点P作QR⊥EF,QR与EF、MN分别相交于Q、R,根据∠MPN=∠EPF=90°,QR⊥ 在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AB=8,BC
.jpg)
已知∠ABC=90°,AB=2,BC=3,AD∥BC,P为线段BD上的动点
2013年4月20日 — 已知∠ABC=90°,AB=2,BC=3,AD∥BC,P为线段BD上的动点,点Q在射线AB上,且满足 PQPC= ADAB(如图1所示).(1)当AD=2,且点Q与点B重合时(如图2所示),求线段PC的长;(2)在图1中,连接AP.当AD= 32,且点Q在线段AB上时,设点B【答案】(1)证明见解析;(2)证明见解析【解析】试题分析:(1)由BC=2AD,点E是BC的中点,可得AD=CE,又由AD∥BC,可得四边形AECD是平行四边形,即可得AE∥CD,继而证得 AOE∽ COF,即可判定AO•OF=OC•OE;(2)易得EF是 BCD的中位线 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC 2016年12月1日 — 如图,AD平行BC,BD平分∠ABC,求证AB=AD 69 (2013?淄博)如图,AD∥BC,BD平分∠ABC.求证: 更多类似问题 > 为你推荐: 特别推荐 “网络厕所”会造成什么影响? 新生报道需要注意什么? 华强北的二手是否靠谱? 癌症 如图,AD‖BC,BD平分∠ABC,求证AB=AD 百度知道2014年5月24日 — 已知,如图,AD平行BC,E是线段CD的中点,AE平分∠BA 356 更多类似问题 > 为你推荐: 特别推荐 “网络厕所”会造成什么影响? 新生报道需要注意什么? 华强北的二手是否靠谱? 癌症的治疗费用为何越来越高 已知 如图,AD平行BC,点E是DC的中点,AE平分角BAD

如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,AB
[答案](Ⅰ)见证明;(Ⅱ)(Ⅲ)[解析]分析]首先利用几何体的特征建立空间直角坐标系(Ⅰ)利用直线BF的方向向量和平面ADE的法向量的关系即可证明线面平行;(Ⅱ)分别求得直线CE的方向向量和平面BDE的法向量,然后求解线面角的正弦值即可;(Ⅲ)首先确定两个半平面的法向量,然后利用二面角的余弦值计算公式 试题分析:(1)由当PQ∥CD时,四边形PQCD为平行四边形,可得方程24t=3t,解此方程即可求得答案;(2)根据PQ=CD,一种情况是:四边形PQCD为平行四边形,可得方程24t=3t,一种情况是:四边形PQCD为等腰梯形,可求得当QCPD=QCEF=QF+EC 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm 25解析:本题考查了切线的判定和性质、全等三角形的判定和 性质、等边三角形的判定和性质以及扇形面积的计算等 (1)观察图形,易得CD与⊙B相切要证明CD与⊙B相切, 因为CD与⊙B没有明确的公共点,所以可利用“ d=r^+ 的方 法证明点B到CD的距离等于⊙B的半径过点B作CD的 垂线段,再利用全等三角形的判定 如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以 如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点,联结DE交边AB于点F,联结AC交DE于点G,且 (1)求证:AB∥CD; (2)如果AD2=DG•D (12分 如图,已知在四边形ABCD中,AD∥BC,E为边CB延长线上一点

如图,已知:梯形ABCD中,AD‖BC,AB⊥BC,AD=CD=5,AB=4
2011年10月10日 — 1因为PE=CE,所以∠C=∠EPC,推出∠APB=∠C所以AP平行DC,那么ADCP是平行四边形 AP=DC=5,用勾股定理算出BP=3 2BP=3,PC=5所以BC固定BC=8 过点D,E分别做垂线垂直BC为F,H点则BF=5,CF=3 利用CE/CD=CH/CF 计算出CH=391.已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD 线上的一点向角的两边作垂线0PB两垂直A一对称2过角平分线上的一点作角平分线的垂线,一平行从而形成等腰三角形; 1.已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC (12分)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD,对角线AC与BD交于点E点F是线段EC上一点,且∠BDF=∠BAC(1)求证:EB2=E 百度试题 结果1 结果2 结果3 题目 (12分)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD,对角线AC与BD交于点E点F是线段 (12分)如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD ∵AD∥BC ,∴∠ADE+∠C=180°,∵∠AFE+∠EFB=180°,∴∠EFB=∠C,∵BE平分∠ABC,∴∠EBF=∠EBC 考点点评: 此题考查了全等三角形的判定与性质以及平行 线的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用 如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于
.jpg)
如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=10cm,AD
分析:(1)用t表示出AP和BQ的长,然后根据梯形的面积公式进行解答, (2)过P作PN⊥BC于N,过D作DM⊥BC于M,根据题干条件求出MC的长,用t表示出QN的长,若梯形PQCD为等腰梯形,则QN=MC,列出等式解出t的值,(3)若 PQC的面积与 PCD的
石灰石工业磨粉机的转动方向
--山东威海市白云石磨粉机现货热销
--广西来宾高龄土加工粉磨设备
--辊式矿石磨粉机的用途
--上海比较有名的雷蒙磨厂上海比较有名的雷蒙磨厂上海比较有名的雷蒙磨厂
--1250重钙磨粉机雷蒙机
--哪厂生产石粉机
--重晶石粉的价格
--粉碎站设备明细序号
--焦作石灰石加气砖机设备
--开个制粉厂需要投资多少
--上海黎明重工矿山
--湖南省衡阳工业磨粉机厂家
--石家庄雷磨机
--上海有限公司雷蒙磨
--沈阳威力200目磨粉机
--时产60吨液压重晶石磨粉机械
--石灰石制粉用什么机器
--承包山林中的国土资源(煤柑石)的合同
--红色粉磨方解石矿
--菌棒绞碎磨细设备
--鄂鱼板型号100*60矿石磨粉机
--辽宁抚顺市白云石微粉磨解决方案
--商混与建筑面积计算
--把石头砸碎造沙子前景
--补挂窑皮操作
--粉磨生产线和预粉磨砂粉同出立磨优优势
--68粉碎器打多少氮气
--合钢矿渣磨
--福建南平市白云石微粉加工设备客户案例
--










